Este problema foi enviado por um visitante do site www.paulomarques.com.br  pedindo a solu��o. Trata-se da quest�o 16 de uma  prova do Simulado da Unicamp - vestibular 2011. Vamos ao enunciado e � resolu��o:

Nota: este � o arquivo de n�mero 400 do site! Este site est� no ar desde 1995! Visite o meu atual provedor www.algosobre.com.br 
o qual gentilmente hospeda o meu site nos seus servidores. 


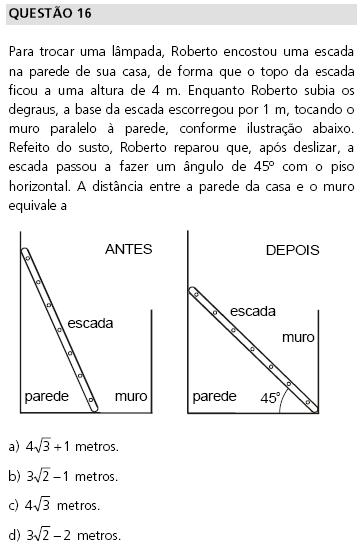
Solu��o:

De forma a facilitar a resolu��o, constru�mos a figura abaixo onde AB = 4.
Seja BC = x ; nestas condi��es, pelo enunciado da quest�o conclu�mos que EF = x + 1, pois a base da escada escorregou 1 metro.

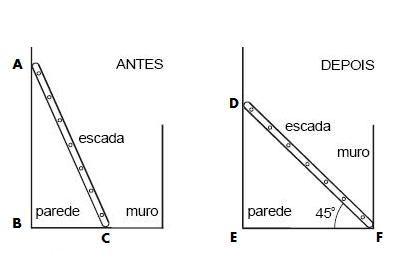
Pela simples observação do triângulo retângulo ABC, poderemos escrever, usando o Teorema de Pit�goras:
4² + x² = AC² 

Como o tri�ngulo DEF � ret�ngulo em E e o �ngulo F � igual a 45� , conclu�mos que o �ngulo D vale tamb�m 45�, o que nos permite afirmar que o tri�ngulo DEF � is�sceles e, por consequ�ncia, DE = EF = x + 1.

Ent�o, aplicando o Teorema de Pit�goras no tri�ngulo DEF, teremos:

(x + 1)² + (x + 1)² = DF²

Lembrando que trata-se da mesma escada (que escorregou 1 metro), � claro que DF = AC.

Ent�o, a igualdade acima pode ser reescrita como:

(x + 1)² + (x + 1)² = AC²

Ent�o, comparando as duas igualdades acima em negrito vermelho  poderemos concluir facilmente que:

4² + x² = (x + 1)² + (x + 1)²

Ora, esta � uma equa��o do segundo grau; vamos resolv�-la:

16 + x² = 2(x + 1)² 
Desenvolvendo o segundo membro, fica:
16 + x² = 2(x² + 2x + 1)
16 + x² = 2x² + 4x + 2
Simplificando e igualando a zero, vem:
x² + 4x - 14 = 0

Aplicando a f�rmula de Bhaskara ,


encontraremos as ra�zes x' = -2 + 3.2^1/2 ou x'' = -2 - 3.2^1/2 
Nota: utilizei expoente para evitar o s�mbolo de raiz quadrada, mais dif�cil de escrever neste momento pelo teclado. Afinal, estou com pressa para assistir o glorioso FLUMINENSE jogando contra o Guarani de Campinas. O FLUZ�O continua l�der do Campeonato Brasileiro!

Observe que a raiz x'' n�o serve ao problema pois � um n�mero negativo e o problema em quest�o refere-se ao c�lculo de
dist�ncia, portanto a resposta deve ser um n�mero positivo.

Ent�o, como a dist�ncia entre a parede e o muro � igual a x + 1, teremos que a dist�ncia procurada ser� igual a:
EF = x + 1 = -2 + 3.2^1/2 + 1 = 3.2^1/2 - 1 

EF = 3.2^1/2 - 1 (3 vezes a raiz quadrada de 2, menos 1).

Ent�o, a alternativa correta � a de letra B.

Veja AQUI um outro problema sobre escadas, um pouquinho mais "puxado" do que este!

Paulo Marques, 05/09/2010 - Feira de Santana - BA

VOLTAR