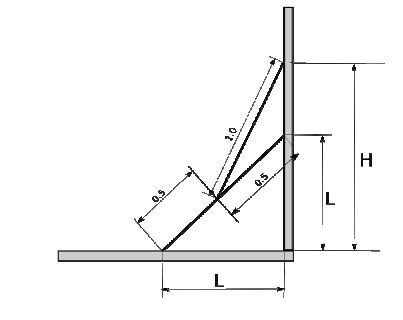
Considere a figura a seguir onde duas escadas foram justapostas na forma indicada. Pede-se determinar as medidas de L e H.

Nota: este problema foi enviado por um visitante do site, pedindo a solução. Ei-la:

Solução:

Se necessário comece revisando Trigonometria.
De forma a facilitar a resolução, construímos a figura abaixo onde CP = H e RP = PB = L. 

Pela simples observação do triângulo retângulo RPB, poderemos escrever, usando o Teorema de Pitágoras: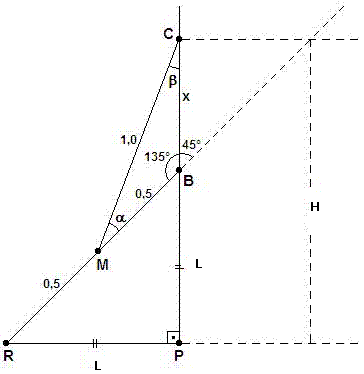
L² + L² = (0,5 + 0,5)² ou seja: 2.L² = 1² , de onde tiramos L²  = 1/2 e, daí vem imediatamente L = √2 / 2, cujo valor aproximado é igual a 0,707.
Observe que o cálculo da medida L foi imediato. Já para o cálculo da medida H, teremos um pouco mais de trabalho mas, vamos lá!
Observe que H = L + BC; como L já é conhecido, vamos calcular BC = x.
Nota: do enunciado, o triângulo retângulo RPB é isósceles e, portanto, os ângulos de vértices R e B são iguais a 45º . Esta conclusão é decorrente de: a soma dos ângulos internos de um triângulo qualquer é igual a 180º.

MB / senβ = 1 / sen135º = x / senα
Como MB = 0,5 = 1/2, vem, substituindo: 0,5 / senβ = 1 / sen135º = x / senα
Lembrando que sen 135º = sen(90º + 45º) = sen90º.cos45º + sen45º.cos90º = √2 / 2
Nota: lembre-se que sen90º = 1 e cos90º = 0 e cos45º = √2 / 2 e, daí, o resultado acima.

Poderemos agora escrever, pela lei dos senos:
(1/2)/(senβ) = 1/(√2 / 2) = x / senα

Como a soma dos ângulos internos de um triângulo plano vale 180º, poderemos escrever em relação ao triângulo MBC:
β + α + 135º = 180º , de onde tiramos β + α = 180º - 135º = 45º e, portanto β = 45º -  α .

Substituindo, fica:
(1/2)/[sen(45º - α)] = 1/(√2 / 2) = x / senα

Observando atentamente as igualdades acima, percebemos que basta calcular o valor de senα , para achar o valor de x e, por consequência o valor de H, já que H = L + x e L já foi calculado. Então, amigos e amigas, o problema está resolvido! Só falta fazer as contas. Vamos lá!

Nota: se fosse com caneta e papel, seria bem tranquilo mas, no teclado, ah no teclado ... 

Inicialmente observe que  
sen(45º - α) = sen45º.cosα - senα.cos45º = (√2 / 2).cosα - senα.(√2 / 2) = (√2 / 2)(cosα - senα)

Nota: lembre-se que sen45º = cos45º = √2 / 2 , o que justifica as substituições acima.

Substituindo, vem:

(1/2)/[(√2 / 2)(cosα - senα))] = 1/(√2 / 2) = x / senα
Temos então as seguintes igualdades:
(1/2)/[(√2 / 2)(cosα - senα))] = 1/(√2 / 2)
1/(√2 / 2) = x / senα

Vamos tratar as duas igualdades separadamente.
Para a primeira, teremos:
(1/2)/[(√2 / 2)(cosα - senα))] = 1/(√2 / 2)
Efetuando as operações indicadas nos dois membros e simplificando, fica:
1 = 2(cosα - senα) ou na forma equivalente: cosα - senα = 1/2

Para a segunda igualdade, teremos:
1/(√2 / 2) = x / senα
Efetuando as operações indicadas nos dois membros e simplificando, fica:
2senα = √2.x

Contamos agora com as duas igualdades, já simplificadas:
cosα - senα = 1/2
2senα = √2.x
Da trigonometria sabemos que: sen²α + cos²α = 1
Logo, como da primeira igualdade tiramos cosα = senα + 1/2 , vem substituindo:
sen²α + (senα + 1/2)² = 1
Desenvolvendo e simplificando a expressão acima, obteremos:
8sen²α + 4senα - 3 = 0
Resolvendo essa equação do segundo grau, obteremos:
senα = (-2 + √28)/8  ou senα = (-2 - √28)/8

Observe-se aqui que a raiz  senα = (-2 - √28)/8 , por ser negativa, não serve ao problema pois, sabemos que o ângulo α é agudo e, portanto, o seno é positivo. Assim, concluímos que:
senα = (-2 + √28)/8

Já sabemos que 2senα = √2.x e precisamos calcular o valor de x. Então, substituindo o valor de senα, teremos:
2[(-2 + √28)/8] = √2.x
Resolvendo a igualdade acima e simplificando, obteremos:
x = (√14 - √2)/4

Ora, já vimos no início do problema que o H procurado (vivo ou morto! eh eh eh ...) é dado por:
H = L + x
O valor de x, calculamos acima e o valor de L é √2/2 conforme vimos no início do problema. Logo, o valor de H será:
H = √2/2 + (√14 - √2)/4
Desenvolvendo e simplificando, obteremos finalmente:
H = (√14 + √2)/4
Usando um calculadora (a do windows serve), encontramos o valor aproximado para H: 1,29 m, o que justifica o título dado ao arquivo. 

Como diriam os meus amigos mineiros: eta probleminha trabalhoso, sô!!! 

Feliz 2010 para todos!

Paulo Marques, 03/01/2010 - Feira de Santana - BA

VOLTAR