A altura de um edifício em Goiás, estado do Atlético-GO, campeão da série C - 2008            
Nota: este problema foi enviado por um visitante do site, pedindo que eu resolvesse. Eis o problema e a solução:

UFG - 2008) Dois observadores, situados nos pontos A e B, a uma distância d um do outro, como mostra a figura abaixo, avistam um mesmo ponto no topo de um prédio de altura H, sob um mesmo ângulo θ com a horizontal.

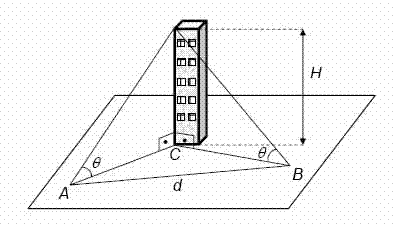
Sabendo-se que o ângulo ABC também mede θ e desconsiderando a altura dos observadores, a altura H do prédio é dada pela expressão:
A)
 
B)


C)


D)

E)
 
Solução:
Observando a figura dada no enunciado, poderemos escrever:

t
tg θ = H / AC = H / BC , de onde concluímos que AC = BC. Portanto, o triângulo ABC é isósceles.
É dito no enunciado que o ângulo ABC (vértice em B) tem medida também igual a θ. Como sabemos que a soma dos ângulos internos de qualquer triângulo é igual a 180 graus, poderemos escrever: θ + θ + C = 180, de onde tiramos C = 180 - 2θ

Aplicando o Teorema dos Cossenos-TC ao triângulo ABC, vem:

d2 = AC2 + BC2 - 2.AC.BC.cos(180 - 2θ)
Lembrando que AC =  BC, vem substituindo:
d2 = AC2 + AC2 - 2.AC.AC.cos(180 - 2θ) 
E simplificando:
d2 = 2.AC2 - 2.AC2 . cos(180 - 2θ)

Colocando o termo comum em evidencia, fica:
d2 = 2.AC2 [1 - cos(180 - 2θ)]

Já vimos acima que tg θ = H / AC, de onde tiramos: AC = H / tg θ
Substituindo na expressão anterior, teremos:

d2 = 2.(H / tg θ)2 [1 - cos(180 - 2θ)]

Sabemos da Trigonometria que cos(180 - a) = - cos a . Então, concluímos que cos(180 - 2θ) = - cos2θ.
Substituindo na expressão acima, teremos:
d2 = 2.(H / tg θ)2 [1 - (- cos2θ)] = 2.(H / tg θ)2 [1 + cos2θ]

Ainda da Trigonometria, sabemos que cos 2θ = 2.cos2 θ - 1 , de onde tiramos: 1 + cos 2θ = 2.cos2 θ
Substituindo este valor na igualdade anterior, teremos:

d2 = 2.(H / tg θ)2 . 2.cos2 θ = 4.(H / tg θ)2 . cos2 θ
Então, temos:
d2 = 4.(H / tg θ)2 . cos2 θ
Extraindo a raiz quadrada de ambos os membros, encontraremos:
d = 2.(H / tg θ) . cos θ ou na forma equivalente: d . tg θ = 2.H. cos θ

Sabemos também que tg θ = sen θ / cos θ . Vem, substituindo:

d . (sen θ / cos θ) = 2.H. cos θ ou na forma equivalente:  d . sen θ = 2.H. cos θ . cos θ

Então, o valor procurado H será igual a:
H = (d . sen θ) /(2. cos θ . cos θ) = (d / 2) . (sen θ / cos θ) . (1 / cos θ) = (d / 2) . tg θ . (1 / cos θ).
Mas, o inverso do cosseno de um arco é igual à secante do mesmo arco ou seja: 1 / cos θ = sec θ.
Teremos então, finalmente a resposta: 

H = (d / 2) . tg θ . sec θ
Portanto, a alternativa correta é a de letra E. 

Paulo Marques, 27 de novembro de 2008 – Feira de Santana - BA 

VOLTAR