|
O sapo e o pernilongo |
Um sapo e um pernilongo encontram-se respectivamente na
origem e no ponto (8, 2) de um sistema cartesiano ortogonal. Se o sapo só pudesse saltar nas direções
positivas dos eixos cartesianos e cobrisse uma unidade de comprimento em
cada salto, o número de trajetórias possíveis para o sapo alcançar o
pernilongo seria igual a:
a) 35
b) 45
c) 70
d) 125
e) 256
Solução:
Considere a figura a seguir, onde está representada em vermelho, uma das
trajetórias possíveis, onde S = sapo e I = pernilongo.
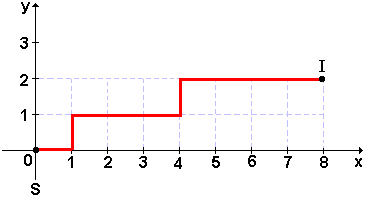
O enunciado diz que o sapo só pode se mover nas direções positivas dos
eixos cartesianos, ou seja, para a direita ou para cima.
Convencionando que um deslocamento para a direita seja indicado por D e
um deslocamento para cima seja indicado por C, o deslocamento indicado na
figura seria representado por DCDDDCDDDD.
Agora resolva este:
Outros deslocamentos possíveis seriam, por exemplo:
DDDDDDDDCC
DDCCDDDDDD
CDDDDDDDDC
etc
Para entender isto, basta observar a figura dada.
Observe que para o sapo alcançar o pernilongo segundo as regras ditadas,
teremos sempre 8 deslocamentos para a direita (D) e 2 para cima (C).
Ora, teremos sempre 10 deslocamentos, sendo 8 para a direita (D)e 2 para
cima (C).
Então, para obter o número total de deslocamentos possíveis, basta
calcular o número de
permutações com repetição dos 10
elementos, observando que existem repetições de 8 e de 2 elementos.
Então, do que já sabemos da Análise
Combinatória, poderemos escrever, finalmente:
P(10; (8,2)) = 10! /(8!.2!) = (10.9.8!) / (8!.2.1) = (10.9) / 2 = 45
Portanto, são 45 trajetórias possíveis, ou seja, alternativa B.
Esta questão compareceu num vestibular da PUC - RS.
Um coelho e um jacaré encontram-se respectivamente na origem e no ponto (9,
3) de um sistema cartesiano ortogonal. Se o coelho só pudesse saltar nas
direções positivas dos eixos cartesianos e cobrisse uma unidade de
comprimento em cada salto, o número de trajetórias possíveis para o
coelho alcançar o jacaré seria igual a:
Resposta: 220 trajetórias possíveis.
Nota: no problema inicial, provavelmente o sapo irá
"traçar" o pernilongo. Já aqui neste problema, acho que
quem vai sobrar é o coelho!...
eh eh eh ...