|
Um termo maior numa soma binomial finita |
Determine
o termo de maior valor do desenvolvimento do Binômio de
Newton (1 + 1/2)1000 .
Solução:
Já sabemos que a fórmula do termo
geral de um Binômio de Newton da forma (a + b)n
é:![]()
Analogamente poderemos escrever:
![]()
Dividindo
membro a membro as igualdades acima, desenvolvendo e simplificando,
chegaremos à expressão abaixo:
![]()
Nota:
recomendamos ao leitor fazer esta verificação; será
um excelente exercício.
Lembretes
necessários:
![]()
O
número acima é conhecido como Número Binomial ou
Número Combinatório.
n! = 1.2.3.4.5.6. ...
(n-1).n (n! = fatorial
de n)
S�o v�lidas as seguintes propriedades, por exemplo:
(p – 1)! = p! / p
onde p � um n�mero natural maior ou igual a 1.
(k + 1)! = k! . (k+1)
onde k � um n�mero natural.
A
fórmula obtida após as simplificações, como j�
vimos, é:
![]()
Observe
que Tp é o termo imediatamente anterior a
Tp+1 .
Ora, para que o termo Tp+1 seja
maior do que o termo Tp , é óbvio que
deveremos ter:![]()
Então,
para determinar o termo de maior valor do desenvolvimento do
binômio
(1 + 1/2)1000 basta determinar o maior
valor inteiro possível para p , que satisfaça à
desigualdade acima.
Voltando ao binômio do problema (1 + 1/2)1000 , temos:
a = 1, b = 1/2 e n = 1000;
substituindo na desigualdade acima, teremos:![]()
Simplificando,
fica:![]()
Como
p é um número inteiro positivo, 2p também será
positivo e, para que a desigualdade acima seja verdadeira, deveremos
ter 1001 – 3p > 0 .
Daí vem: 1001 – 3p >
0 , ou seja, 1001 > 3p
logo,
3p < 1001 o que nos leva a p < 1001/3
Então
p < 333,6 e, como p é inteiro, vem finalmente p = 333.
Como
o valor máximo possível para p é
333, teremos que Tp+1 será o termo T334
, e este é o maior termo do desenvolvimento do binômio
(1 + 1 /2)1000 .
Portanto, o maior termo do
desenvolvimento do binômio proposto será o de ordem 334,
ou seja, o 334º termo.
Para determinar qual é este
termo, basta usar a fórmula do termo
geral do binômio de Newton vista acima, ou
seja: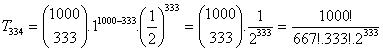
É claro que esta questão é um desafio, e
portanto requer que o estudante esteja familiarizado com as técnicas
de cálculo dos números
binomiais e dos fatoriais.
Caso contrário, o exercício tornar-se-á deveras
penoso!
Agora resolva este:
Qual o maior termo
no desenvolvimento de (1 + 1/4)10 ?
Resposta:
o maior termo é o terceiro e é igual a
45/16.
Paulo
Marques - Feira de Santana - BA - 02 de novembro de 2002, revisado em 10/11/2006.