Enchendo o tanque no carnaval da Bahia de 2007

NOTA
A resolução desta questão requer noções de derivadas, assunto do primeiro ano na Universidade, na área de Ciências Exatas.

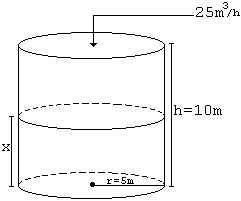
Um tanque tem a forma de um cilindro circular reto de raio da base r = 5m e altura h = 10m. No tempo t = 0, o tanque começa a ser enchido com água, que entra no tanque com uma vazão de 25 m³/h. Com qual velocidade o nível da água sobe? Depois de quanto tempo o tanque estará cheio?

SOLUÇÃO:

Veja a figura abaixo:

Já sabemos que o volume de um cilindro reto de raio da base R e altura h é dado pela fórmula V = p.R².h

Sendo x o nível da água no tanque, é óbvio que poderemos escrever:

V = p.5².x = 25.p.x  (1)
A vazão de 25 m³/h é justamente a derivada  dV/dt.

Derivando a expressão (1) em relação a x, vem imediatamente:
dV/dx = 25p

Derivando a expressão (1) em relação à variável t, vem:

Ora, a velocidade v com que o nível da água sobe é, exatamente dx/dt.
Substituindo os valores conhecidos, vem finalmente:

25 = 25p .v, de onde tiramos  v = 1/p m/h ou aproximadamente,  v = 0,318 m/h.

Portanto, o nível da água sobe à uma razão de 0,318 metros por hora.

O tempo que levará para encher o tanque será então:
T = 10m / 0,318 m/h = 31,4h = 31h + 0,4h = 31h + 0,4.60min
T = 31 horas e 24 minutos.

Paulo Marques – Feira de Santana – 27 de maio de 2001.  Revisado e ampliado em 18/02/2007.

VOLTAR
CONTINUAR