Nota: os enunciados dos dois problemas a seguir, foram enviados por um visitante do site. Como nem sempre tenho tempo de responder a todos os e-mails que recebo, normalmente publico as soluções solicitadas na forma de arquivo. Tenho procedido assim já há muito tempo pois, entendo que universalizando as soluções no site, estarei ajudando a um número maior de pessoas. Este é o 310º arquivo publicado no site, que este ano estará completando 10 anos! Sim, os primeiros arquivos foram publicados em 1995, embora em outro provedor! Lembrem-se que em 1995 a INTERNET estava apenas começando no BRASIL.
1 Determine o menor número inteiro positivo que dividido por 39 dá resto 16 e dividido por 37, dá resto 36.
Solução:
Sendo D o dividendo , d o divisor, q
o quociente e r o resto, sabemos que D = d.q + r , onde
D, d , q e r são números naturais com 0 £
r < d . Esta relação é conhecida como Teorema de Euclides (filósofo e matemático grego
do século III A.C.).
Podemos então escrever, sendo D o número inteiro positivo procurado:
D = 39q + 16
D = 37q' + 36, onde D é o dividendo procurado e q e q' são os
respectivos quocientes.
Observe que as expressões acima são da forma y = ax + b cuja representação gráfica dos pontos (x,y) no plano cartesiano é uma reta para a, b, x e y reais. Como as igualdades acima estão definidas em N – conjunto dos naturais, evidentemente que as representações gráficas não serão retas (contínuas), porém os pontos determinados pelos pares ordenados (q, D) ou (q',D) serão pontos colineares ou seja, alinhados.
Posto isto, podemos considerar q e q' como sendo a variável independente x (por analogia com a equação da reta y = ax + b) e, D como a variável dependente y e escrever o seguinte sistema de equações:
y = 39x + 16
y = 37x + 36
lembrando que estamos considerando aqui apenas os valores inteiros positivos
das variáveis x e y.
Agora, basta resolver o sistema acima e achar o valor de
y = D.
Subtraindo membro a membro as igualdades acima, fica:
y – y = (39x + 16) – (37x + 36)
0 = 39x + 16 – 37x – 36
0 = 2x – 20, de onde tiramos x = 10.
Substituindo em qualquer uma das equações, teremos finalmente:
y = 39x + 16 = 39.10 + 16 = 390 + 16 = 406.
Ora, já sabemos que y = D e, portanto, o número procurado é igual a 406.
Verifique que de fato, 406 dividido por 39 dá 10 e resto 16 e que também 406 dividido por 37 dá 10 e resto 36.
Nota: uma vez entendida a metodologia acima, poderemos
resolver o mesmo problema usando a seguinte forma prática:
Como D = 39q + 16 e D = 37q' + 36
Podemos escrever D = 39q + 16 = 37q' + 36
Fazendo q = q' e substituindo: 39q + 16 = 37q + 36 de
onde vem q = 10.
Nota: fazendo q = q' , obteremos apenas uma
solução do problema, ou seja, a menor solução inteira positiva pedida no
enunciado.
Substituindo, vem finalmente D = 39.10 + 16 = 406
, que é o menor número inteiro positivo que satisfaz ao problema
proposto.
Generalizando ...
Se a pergunta fosse:
quais
os números naturais que divididos por 39
deixam
resto 16 e divididos por 37, deixam resto 36 , o
problema teria infinitas soluções. Veja a seguir, a solução
apresentada para este caso generalizado, pelo ilustre visitante do site,
Hélio M. Fragoso, publicada com a devida permissão:
Seja N o número procurado. Chamemos de q1 e q2
os quocientes da divisão de N por 39 e 37, respectivamente.
Segundo o enunciado do problema, teremos:
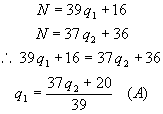
Sendo q1 um
número inteiro, o numerador da fração acima deve ser múltiplo do
denominador. Logo,
![]()
onde n é um número inteiro.
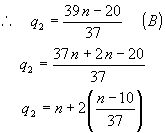
Como q2 é um
número inteiro, a expressão entre parêntesis deve também ser um número
inteiro, que chamaremos de k.
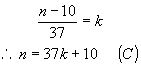
![]()
Substituindo
(B) em (A) resulta:

Substituindo q1 da
expressão (D) na igualdade inicial
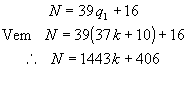
Fazendo k = 0, k = 1, k = 2 etc.
obtemos os valores de N que satisfazem às condições do problema.
2 Resolver a equação 8x + 12y = 23, de modo que x e y sejam positivos e sua soma, um número inteiro.
Solução:
Tirando o valor de y fica: y = (23 – 8x) / 12
O problema pede que x + y seja um número inteiro com a condição de que x e y sejam positivos. Teremos então, substituindo o valor de y:
x + (23 – 8x) / 12 = (12x) / 12 + (23 – 8x) / 12 = (4x + 23) / 12
O problema impõe a condição que a soma acima seja um
número inteiro. Portanto, o numerador 4x + 23 deve ser um múltiplo de
12 ou seja: 4x + 23 = 12k onde k é um inteiro. Daí tiramos
x = (12k – 23) / 4 . Lembrando que x deve ser positivo, conforme dito no
enunciado da questão, deveremos também ter x = (12k – 23) / 4 > 0 , o
que resulta 12k – 23 > 0 ou 12k > 23 ou k > 23/12 ou seja k >
1,916... .
Como k é inteiro, os valores possíveis para k serão k = 2, 3, 4,
5, 6, ...
Como y = (23 – 8x) / 12 , vem substituindo o valor de x obtido acima:
y = [23 – 8(12k – 23)/4] / 12 = [(23 – 24k + 46)] / 12 = (69 – 24k) / 12
Lembrando que o problema impõe que y deve ser positivo, deveremos ter:
y = (69 – 24k) / 12 > 0, o que resulta 69 – 24k
> 0 ou 69 > 24k ou 24k < 69, o que resulta
k < 2,875. Como k é inteiro, deveremos ter k = 2, 1, 0, -1, -2, -3, ... .
Portanto para que x seja positivo vimos acima que k = 2,
3, 4, 5, ... e para que y seja positivo vimos também que
k = 2, 1, 0, -1, -2, -3, ... . Para que ambos sejam positivos, deveremos ter
evidentemente k = 2, que é o único valor de k que atende
simultaneamente às duas condições.
Portanto, como k = 2, os números procurados serão obtidos substituindo o valor de k nas expressões obtidas acima:
x = (12k – 23) / 4 = (12.2 – 23) / 4 = (24 – 23) / 4 = 1/4
y = (69 – 24k) / 12 = (69 – 24.2) / 12 = (69 – 48) / 12 = 21/12
Resposta: x = 1/4 e y = 21/12.
Nota: observe que x e y
satisfazem ao enunciado pois são ambos positivos e a soma resulta num número
inteiro, ou seja: (1/4) + (21/12) = (3/12) + (21/12) = 24/12 = 2. Além disso,
substituindo x e y na equação original resulta
8(1/4) + 12(21/12) = 2 + 21 = 23.
Agora resolva estes:
1) Determinar o menor número
inteiro positivo que dividido por 40 dá
resto 18 e dividido por 38, dá resto 26.
Resposta: 178
2) Determinar os números
naturais que divididos por 40 deixam
resto 18 e divididos por 38, deixam resto 26.
Resposta: números da forma 760k + 178, onde k
= 0, 1, 2, 3, 4, ... .
Veja a solução clicando AQUI. Para
retornar à esta página, após visitar a solução, clique em retornar no seu
browser (navegador).
3) Resolver a equação 6x + 10y = 21, de modo que x e y
sejam positivos e sua soma um número inteiro.
Resposta: x = 9/4 e y = 3/4.