Dois mil e quatrocentos funcionários com mais de 30 anos.

UNICAMP) Uma empresa tem 5000 funcionários. Desses, 48% têm mais de 30 anos, 36% são especializados e 1400 têm mais
de 30 anos e são especializados. Com base nesses dados, pergunta-se:

a) Quantos funcionários têm menos de 30 anos e não são especializados?
b) Escolhendo um funcionário ao acaso, qual a probabilidade de ele ter até 30 anos e ser especializado?

Nota: este problema foi enviado por um visitante do site, solicitando a solução. Ei-la.

Solução:

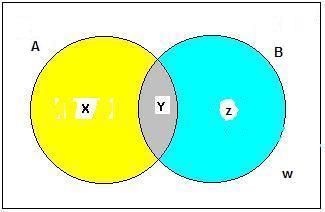
Veja a figura a seguir, onde x, y e z representam número de elementos nos conjuntos A e B, sendo A o conjunto dos funcionários
com mais de 30 anos, B o conjunto dos funcionários especializados e w o número de elementos do conjunto complementar de AUB
(A unido a B) ou seja, w é o número de empregados não especializados e que têm até 30 anos. Lembre-se que "os funcionários especializados" compõem o conjunto B (pintado de azul e cinza)  e "os funcionários com mais de 30 anos" compõem o conjunto A (pintado de amarelo e cinza).


Do enunciado poderemos concluir o que segue:

x + y + z + w = 5000 [total de funcionários da empresa].
x + y = 48% de 5000 = 0,48.5000 = 2400 [lembre que A é o conjunto daqueles funcionários com mais de 30 anos].
y + z = 36% de 5000 = 0,36.5000 = 1800 [lembre que B é o conjunto dos funcionários especializados].
y = 1400 [ a interseção dos conjuntos A e B representa o conjunto dos funcionários especializados e que têm mais de 30 anos].

Em resumo:

x + y + z + w = 5000
x + y = 2400
y + z = 1800 
y = 1400 

Então, por mera substituição, teremos: 1400 + z = 1800, de onde tiramos z = 400.
Analogamente, de x + y = 2400 vem: x + 1400 = 2400, de onde tiramos x = 1000.
Como x = 1000, y = 1400 e z = 400, vem substituindo na primeira igualdade:
1000 + 1400 + 400 + w = 5000, de onde tiramos w = 2200.

Olhando a figura e observando os resultados obtidos acima, x = 1000, y = 1400, z = 400 e w = 2200,

poderemos agora responder às duas questões:
a) Quantos funcionários têm menos de 30 anos e não são especializados?
Verificamos que w é o número procurado ou seja, w = 2200.

b) Escolhendo um funcionário ao acaso, qual a probabilidade de ele ter até 30 anos e ser especializado?
Verificamos que apenas z funcionários possuem até 30 anos E são especializados. Já sabemos que z = 400 e, como o número total de funcionários é igual a 5000, a probabilidade procurada será igual a 400/5000 = 0,08 = 8%.

Nota: o título do arquivo "2400 funcionários com mais de 30 anos" foi escolhido por mim, pois o conjunto A possui exatamente x+y = 2400 elementos.

Agora resolva estes:

1) Escolhendo um funcionário ao acaso, qual a probabilidade de ele ter até 30 anos e não ser especializado?
Resposta: 44%

2) Foi feita uma pesquisa sobre a preferencia de um grupo de pessoas por determinado tipo de música, e concluiu-se que:
43 pessoas gostavam de SAMBA.
6 pessoas gostavam apenas de ROCK.
15 pessoas gostavam de SAMBA e ROCK.
8 pessoas gostavam de ROCK e JAZZ.
13 pessoas gostavam de SAMBA e JAZZ.
3 pessoas gostavam apenas de ROCK e JAZZ.
40 pessoas não gostavam de ROCK.
Ninguém gostava apenas de JAZZ.

VOLTAR