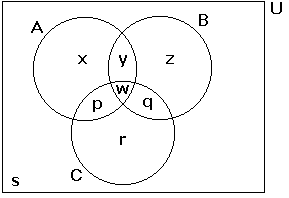
Pelo enunciado e observando a figura acima, poderemos escrever:
x + y + w + p = 43 (número de pessoas que gostam de SAMBA).
z = 6 (número de pessoas que gostam apenas de ROCK)
y + w = 15 (número de pessoas que gostam de SAMBA e ROCK).
w + q = 8 (número de pessoas que gostam de ROCK e JAZZ).
p + w = 13 (número de pessoas que gostam de SAMBA e JAZZ).
q = 3 (número de pessoas que gostam de ROCK e JAZZ).
x + p + r + s = 40 (número de pessoas que não gostam de ROCK).
r = 0 (ninguém gostava apenas de JAZZ).
Substituindo os valores conhecidos nas igualdades acima, vem:
Como q = 3, vem de w + q = 8 que w = 5.
Como y + w = 15 e w = 5, vem que y = 10.
Como w = 5 e p + w = 13, vem que p = 8.
Ora, como y = 10, w = 5 e p = 8, vem de x + y + w + p = 43 que:
x + 10 + 5 + 8 = 43 \ x = 20.
Substituindo os valores conhecidos na igualdade x + p + r + s = 40, vem:
20 + 8 + 0 + s = 40 \ s = 12.
Resumindo os valores encontrados:
x = 20, y = 10, z = 6, w = 5, p = 8, q = 3, r = 0 e s = 12.
Vamos analisar cada alternativa, utilizando os valores conhecidos acima:
(01) 86 pessoas foram consultadas.
O número total de pessoas consultadas será igual a x + y + z + w + p + q + r + s.
Substituindo os valores conhecidos, vem:
20 + 10 + 6 + 5 + 8 + 3 + 0 + 12 = 64
Portanto, a alternativa (01) é falsa.
(02) 24 pessoas gostavam de ROCK.
Sendo B = {gostam de ROCK} , o número total de pessoas que gostam de ROCK será igual a
y + z + q + w = 10 + 6 + 3 + 5 = 24
Portanto, a alternativa (02) é verdadeira.
(04) 36 pessoas gostavam de SAMBA ou ROCK, mas não gostavam de JAZZ.
Sendo A = {gostam de SAMBA}, B = {gostam de ROCK} e C = {gostam de JAZZ}, vemos pela figura anterior que o número de pessoas que gostam de SAMBA ou ROCK mas não gostam de JAZZ será igual a x + y + z = 20 + 10 + 6 = 36
Portanto, a alternativa (04) é verdadeira.
(08) 21 pessoas gostavam de pelo menos dois tipos de música.
A expressão “gostavam de pelo menos dois tipos de música” significa neste caso: “gostam de duas ou três tipos de música”. Olhando a figura acima, concluímos que este número é igual a
y + p + q + w = 10 + 8 + 3 + 5 = 26
Portanto, a alternativa (08) é falsa.
(16) 12 pessoas não gostavam de nenhum dos três tipos de música citadas.
Pela figura acima, vemos imediatamente que o número de pessoas que não gostavam de nenhum dos 3 tipos de música é igual a s.
Já vimos acima que s = 12.
Portanto, a alternativa (16) é verdadeira.
Resposta: 02 + 04 + 16 = 22
Clique AQUI para VOLTAR ao arquivo anterior.
Paulo Marques, 16 de outubro de 2004 - Feira de Santana - BA.