-
UFBA
1986) Uma pesquisa realizada com um grupo de pessoas revelou a
seguinte preferencia pelas revistas A, B e C:
109 lêem a
revista A ;
203 lêem a revista B ;
162 lêem a
revista C ;
41 lêem as revistas B e C;
28
lêem as revistas A e C;
5 lêem as três
revistas
115 não lêem revista.
Das
informações conclui-se:
(01) 500 pessoas foram
consultadas.
(02) 51 pessoas lêem somente a revista A.
(04)
176 pessoas não lêem as revistas B ou C.
(08) 94
pessoas lêem pelo menos duas revistas.
(16) 223 pessoas lêem
as revistas A ou B e não lêem a revista
C.
Solução:
Esta
modalidade de questão na UFBA – Universidade Federal da
Bahia - consiste em identificar as respostas corretas e somar os
valores associados a cada uma delas, marcando o resultado na Folha de
Respostas.
Veja a figura a seguir, onde x, y, z, w, p, q, r
e s representam número
de elementos:
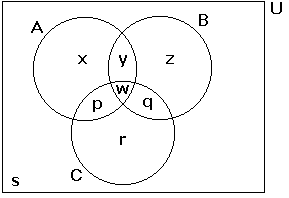
Do
enunciado poderemos concluir o que segue:
x
+ y + w + p = 109 (número de pessoas que lêem a revista
A).
y + z + q + w = 203 (número de pessoas que lêem
a revista B).
p + w + q + r = 162 (número
de pessoas que lêem a revista C)
y + w = 25 (número
de pessoas que lêem as revistas A e B)
w
+ q = 41 (número de pessoas que lêem as revistas B e
C).
w + p = 28 (número de pessoas que lêem as
revistas A e C).
w = 5 (número de
pessoas que lêem as revistas A, B e C).
s = 115
(número de pessoas que não lêem revista).
De
w = 5 e w + p = 28, vem que 5 + p = 28 \
p = 23.
De w = 5 e w + q = 41, vem que 5 + q = 41 \
q = 36.
De w = 5 e y + w = 25, vem que 5 + y = 25 \
y = 20.
Substituindo os valores de p, q, w e y nas igualdades
anteriores, fica:
x + y + 5 + 23 = 109 \
x + y = 81
20 + z + 36 + 5 = 203 \
z = 142
23 + 5 + 36 + r = 162 \
r = 98
Vamos analisar cada alternativa, utilizando os
valores já encontrados acima:
(01)
500 pessoas foram consultadas.
Observe pela figura que o
número total de pessoas consultadas será igual à
soma
x + y + z + w + p + q + r + s = (x + y) + z + w + p + q + r
+ s
Substituindo os valores conhecidos, vem:
81 + 142 + 5 + 23
+ 36 + 98 + 115 = 500
Portanto, a alternativa (01) é
correta.
(02) 51 pessoas lêem somente a revista
A.
Observe na figura acima que o número de pessoas que
lêem somente a revista A é exatamente igual a x. Vimos
acima que x + y = 81 e que y = 20.
Logo, x + 20 = 81 \x
= 61.
Portanto a alternativa (02) é falsa.
(04)
176 pessoas não lêem as revistas B ou C.
Observe
que o número de pessoas que não lêem as revistas
B ou C, é igual à soma x + s ou seja como x = 61 e s =
115, vem: x + s = 61 + 115 = 176
Portanto a alternativa (04) é
verdadeira.
(08) 94 pessoas lêem pelo menos duas
revistas.
A expressão “lêem pelo menos duas
revistas” significa “lêem duas ou três
revistas”
Olhando a figura vemos que o número
de pessoas que lêem pelo menos duas revistas é igual a y
+ p + q + w = 20 + 23 + 36 + 5 = 84
Portanto a alternativa (08)
é falsa.
(16) 223 pessoas lêem as revistas
A ou B e não lêem a revista C.
Observe que o
número de pessoas que lêem as revistas A ou B e não
lêem a revista C é igual x + y + z = 61 + 20 + 142 = 223
Portanto, a alternativa (16) é verdadeira.
Somando
os valores das alternativas verdadeiras: 01 + 04 + 16 = 21,
número que deveria ser marcado na Folha de Respostas.
Agora
resolva este:
Foi feita uma pesquisa sobre a
preferencia de um grupo de pessoas por determinado tipo de música,
e concluiu-se que:
43 pessoas gostavam de SAMBA.
6 pessoas
gostavam apenas de ROCK.
15 pessoas gostavam de SAMBA e ROCK.
8
pessoas gostavam de ROCK e JAZZ.
13 pessoas gostavam de SAMBA e
JAZZ.
3 pessoas gostavam apenas de ROCK e JAZZ.
40 pessoas não
gostavam de ROCK.
Ninguém gostava apenas de JAZZ.
Podemos
concluir que:
(01) 86 pessoas foram consultadas.
(02) 24
pessoas gostavam de ROCK.
(04) 36 pessoas gostavam de SAMBA ou
ROCK, mas não gostavam de JAZZ.
(08) 21 pessoas gostavam de
pelo menos dois tipos de música.
(16) 12 pessoas não
gostavam de nenhum dos três tipos de música
citadas.
Resposta: Somente as afirmativas (02), (04) e
(16) são verdadeiras. Logo, deveria ser marcado na Folha de
Respostas o número 02 + 04 + 16 = 22
Clique
AQUI para ver a solução.
Paulo
Marques, 16 de outubro de 2004 - Feira de Santana - BA.
VOLTAR
