De um jeito mais fácil

Vamos calcular a soma das n parcelas
1 + 11 + 111 + 1111 + ... + 11... 1111, onde o último termo possui n algarismos - visto no exercício anterior - de um jeito mais tranqüilo e muito mais fácil. O método anterior, foi também uma viagem importante, porém, muito longa. Entretanto, o caminho adotado na solução anterior, nos proporcionou reflexão e conhecimento.
Sigamos em frente, então.
Já vimos que a soma
9 + 99 + 999 + 9999 + ... + 99...9999
é dada pela fórmula

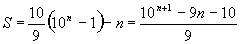
Observando que 9 + 99 + 999 + ... + 99...999 = 9 (1 + 11 + 111 + ... + 11...111) e substituindo o primeiro membro pela fórmula acima, fica:

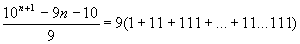
Daí, tirando o valor da soma 1 + 11 + 111 + ... + 11...111 da igualdade acima, resulta finalmente:



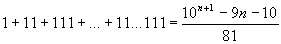
Uma conclusão interessante tirada da fórmula acima é que para todo n natural maior ou igual a 1, o número 10ⁿ⁺¹ – 9n – 10 é um número divisível por 81. Isto é óbvio, já que a soma 1 + 11 + 111 + ... + 11...111 resulta sempre num número natural.

Agora resolva este:

Calcule a soma S = 3 + 33 + 333 + 3333 + ... + 33...3333 que contém n parcelas, onde o último termo possui n algarismos.

Resposta: S = (1/27)(10ⁿ⁺¹ – 9n – 10)

Paulo Marques, 21 de julho de 2002 – Feira de Santana – BA.

VOLTAR