Considere um triângulo ABC cujo ângulo BAC = 75º . Seja D um ponto sobre o lado AB de maneira que o ângulo BCD seja igual a 15º . Determine o valor do ângulo ABC sabendo que AD = 2.BD.

Nota: este problema foi enviado por um visitante do site, pedindo a solução. Ei-la:

Solução:

Se necessário comece revisando Trigonometria.
De forma a facilitar a resolução, construímos a figura abaixo onde AD = 2m e BD = m, conforme o enunciado. 

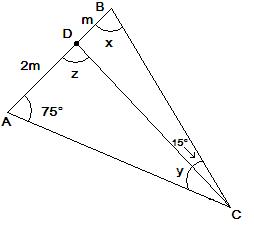
Como a soma dos ângulos internos de um triângulo é igual a 180º, é válido escrever em relação ao triângulo ABC acima:
75º + x + (y + 15º) = 180º . daí, tiramos: x + y = 90º .

Vamos agora aplicar a lei dos senos ao triângulo ADC. Teremos:
2m / seny = CD / sen 75º , de onde tiramos: 

CD = 2m.sen75º / seny   (igualdade I)

Aplicando a mesma lei dos senos agora ao triângulo DBC, teremos:

CD / senx = m / sen15º , de onde tiramos: 

CD = m.senx / sen15º   (igualdade II)

Comparando as igualdades I e II acima, poderemos escrever:

2m.sen75º / seny = m.senx / sen15º
Sabemos da propriedade das proporções que se A/B = C/D então A.D = B.C (propriedade fundamental das proporções: o produto dos meios é igual ao produto dos extremos).
Então, neste caso, poderemos escrever:
2.m.sen75º.sen15º = seny.m.senx , de onde tiramos: 

senx.seny = 2.sen75º.sen15º   (igualdade III)

Ora, os ângulos 75º e 15º são complementares pois sua soma vale 90º. Aqui, vale recordar que se A e B são dois ângulos complementares (A + B = 90º), poderemos sempre escrever: senA.senB = senA.cosA. Com efeito, se A + B = 90º , então 
B = 90º - A e, portanto, senA. senB = senA.sen(90 - A). Ocorre que sen(90 - A) = cosA (o seno de um ângulo é igual ao cosseno do seu complemento - e vice-versa). Aí fica: senA.senB = senA.cosA.

Assim, fazendo A=15º e B=75º , teremos: 2.sen15º.sen75º = 2. sen15º .cos15º
Ora, 2.senp.cosp = sen(2p) como sabemos da Trigonometria; vem, então que 2. sen15º .cos15º = sen(2.15º) = sen30º.

Mas, sabemos que sen30º = 1/2.

Voltando à igualdade III, teremos então:
senx.seny = 2.sen15º.sen75º = sen30º = 1/2, ou seja:

senx.seny = 1/2

Observe que o problema pede para calcular o valor do ângulo x. Como x e y são complementares, vale aqui a mesma propriedade anterior ou seja: senx.seny = senx.sen(90º - x) = senx.cosx 

Temos pois, substituindo: senx.cosx = 1/2, de onde vem: 2.senx.cosx = 1 ou na sua forma equivalente: sen2x = 1.
Como já vimos que x+y = 90º , então podemos afirmar categoricamente que x e y são ângulos agudos e, portanto, poderemos escrever, lembrando que 1 = sen90º: 
sen2x = sen90º .
Esta equação trigonométrica  sen2x = sen90º possui infinitas soluções em R - conjunto dos números reais. Mas, como estamos falando em ângulos agudos, é lícito escrever neste caso: 2x = 90º , de onde tiramos finalmente x = 45º .

Resposta: o ângulo ABC (vértice em B) mede 45º .

Paulo Marques, 25/01/2010 - Feira de Santana - BA

VOLTAR