Considere um certo experimento
aleatório que é repetido n
vezes nas mesmas condições. Seja U
o espaço amostral desse experimento e A
um evento desse espaço
amostral.
Seja A’
o evento complementar
do evento A.
Já
sabemos que:
1) p(A) = n(A) / n(U) [fórmula fundamental das
probabilidades]
2) p(A) + p(A’) = 1 Þ
p(A’) = 1 – p(A)
Para simplificar o
desenvolvimento que faremos a seguir, vamos introduzir a seguinte
notação:
Probabilidade de ocorrer o evento A = p(A)
= p
Probabilidade de
ocorrer o evento complementar A’ = p(A’) = q
Podemos
escrever: p + q = 1 \ q = 1
– p
Não é difícil demonstrar que:
Se o experimento for repetido n vezes nas mesmas condições, então, a probabilidade do evento A ocorrer exatamente k vezes será dada pela fórmula:
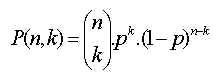
Onde:
P(n,k) =
probabilidade de ocorrer exatamente k
vezes o evento A após n
repetições.
![]()
Exemplo:
Lança-se
um dado 8 vezes. Qual a probabilidade de sair exatamente 5 números
iguais a 3?
Solução:
Sejam
os eventos:
Evento A: sair o número 3
Evento
complementar de A = A’: não sair o número
3
Teremos:
p(A) = 1/6 = p
p(A’) = 1 – 1/6 =
5/6
Portanto, a probabilidade procurada será dada por:
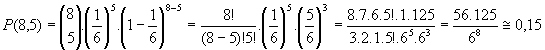
Resposta: a probabilidade de sair o número 3 exatamente 5 vezes no lançamento de um dado 8 vezes, é aproximadamente igual a 0,15 ou 15%.
Agora
resolva este:
Uma
moeda é lançada dez vezes consecutivas. Calcule a
probabilidade de sair exatamente duas caras.
Resposta:
aproximadamente 4,39% (ou 45/1024).
Paulo Marques - Feira de Santana – BA – arquivo revisado em 02/01/2001.