Considere que duas pessoas A e B marcaram um
almoço em determinado restaurante, da seguinte maneira: ambas se comprometem a chegar ao
local acordado entre 12 e 13 horas e esperar o outro por 15 minutos, indo embora
caso a outra pessoa não apareça nesse intervalo de tempo de espera. Nessas
condições, pede-se calcular a probabilidade do encontro marcado ocorrer
entre 12 e 13h.
Nota:
este problema foi enviado para solução por um visitante do
site.
Solução: o
gráfico abaixo, indica as situações que podem ocorrer: A chegando
entre 12 e 13h e esperando 15 minutos (eixo horizontal), até 13:15h e B,
(eixo vertical) igualmente.
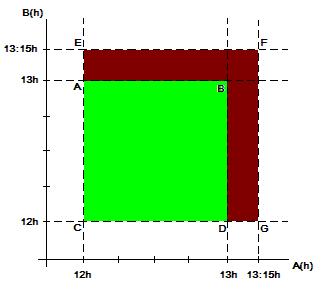
É razoável supor que as probabilidades associadas aos eventos
"encontro das duas pessoas no horário previsto (entre 12 e 13h)"[em
cor verde] e o evento "encontro entre 13h e 13:15" [em cor grená],
sejam proporcionais às áreas respectivas indicadas no gráfico.
Então, como o quadrado verde possui lado igual a 1 (13h - 12h = 1h), sua área
será igual a S1 = 12 = 1.
Já o quadrado maior (CEFG) possui lado igual a 1,25 [observe que 13:15h = 13h +
15minutos = 13,25h e (13,25h - 12h = 1,25h)]. Então, a área do quadrado CEFG
será igual a S2 = 1,252 = 1,5625
Logo, poderemos concluir que a probabilidade P do encontro ocorrer entre 12 e
13h será igual ao
quociente: P = 1/1,5625 = 0,64 = 64%
Resposta: a probabilidade do encontro ocorrer entre 12 e 13h é igual a 64%.
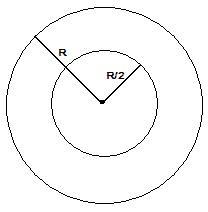
Agora resolva este: qual a probabilidade de um ponto escolhido ao acaso num
círculo de raio R, se situar mais próximo da circunferência do que do centro?
Veja a figura a seguir, que fornece uma pista para a solução. A resposta é 75%.
Notas:
1) Com efeito, o ponto escolhido estará mais próximo da circunferência de raio R, se ele estiver a uma distância maior do que R/2 do centro.
Então, calculando a probabilidade p do ponto se situar dentro do círculo menor (de raio R/2) teremos: p = área do círculo menor/área do círculo maior = 0,25.
Logo, a probabilidade do ponto estar fora do círculo menor será igual à probabilidade complementar ou seja: 1 - 0,25 = 0,75 = 75%.
2) Lembre-se que a área S de um círculo de raio igual a x é dada por: S = pi.x2 onde pi é o número irracional de valor aproximado 3,14.
Paulo Marques - Feira de Santana – BA – 24/04/2011. Editado em 10/08/2013.