Noções elementares de Estatística: medidas de tendência central e de dispersão

1 – Introdução

No Novo Dicionário Brasileiro – Ed. Melhoramentos – 7ª edição – 1971 lê-se para o verbete estatística -  1. conjunto de processos que tem por objeto a observação, classificação formal e análise dos fenômenos coletivos ou de massa, bem como a indução das leis a que tais fenômenos globalmente obedeçam. 2. apresentação numérica, em tabelas ou gráficos, dos resultados da observação de fenômenos de massa. Claro que o termo massa , refere-se à população e não ao conceito físico.

Os dados estatísticos devem ser apresentados na forma de tabelas, de modo a facilitar a sua interpretação. Imaginemos por exemplo o conjunto de valores a seguir, coletados numa sala de aula com 32 alunos, referente às idades dos alunos em anos:

17, 17, 17, 18, 18, 18, 18, 18,
19, 19, 19, 19, 19, 20, 20, 20,
20, 20, 20, 20, 21, 21, 21, 21,
21, 21, 21, 21, 22, 22, 23, 23.

Nota: dados expressos desta forma são ditos dados não agrupados.

Poderemos representar estes dados de uma forma mais organizada, conforme tabela a seguir, onde a coluna frequência representa o número de ocorrências de cada idade:

Idade (a)	Freqüência
17	3
18	5
19	5
20	7
21	8
22	2
23	2
Total	32

Observem que a apresentação dos dados na forma de tabela facilita e muito a interpretação.

Considere agora a relação dos pesos (em kg) de 30 alunos de uma sala, indicada a seguir:

75 – 68 – 75 – 59 – 68 – 80 – 84 – 68 – 80 – 68
68 – 75 – 75 – 80 – 80 – 75 – 80 – 68 – 84 – 75
68 – 59 – 68 – 80 – 80 – 68 – 80 – 75 – 68 – 80

Observem que estes dados não agrupados, podem até causar confusão para sua interpretação. E vejam que são somente 30 alunos; imaginem se fossem 3000?  Vejam os mesmos dados agrupados conforme tabela abaixo:

Peso (kg)	Freqüência (f)
59	2
68	10
75	7
80	9
84	2
Total	30

É evidente que a representação na forma de tabela é muito mais conveniente para qualquer análise que se deseje fazer em relação aos dados. O uso de tabelas (dados agrupados) é muito difundido em Estatística.

Os mesmos dados acima, poderiam ser agrupados com os pesos em classes de 10 em 10 kg, da seguinte forma:

Peso (em kg)	Freqüência
50 |---- 60	2
60 |---- 70	10
70 |---- 80	7
80 |---- 90	11
Total	30

Notas:
a) claro que poderíamos dividir os pesos de 5 em 5kg, 6 em 6kg, etc. Estes intervalos são denominados classes. 
b) o símbolo |--- significa que o extremo 50 pertence ao intervalo e o extremo 60 não pertence ao intervalo. Por exemplo, se quiséssemos indicar que o valor 60 pertence ao intervalo, escreveríamos: 50|---|60. (Os pontos tracejados devem ser escritos de forma contínua; não encontrei símbolo para isto no teclado).

Na Estatística, a representação dos dados através de tabelas é bastante comum. Estes dados tabulados são conhecidos como distribuições de frequência.

2 – Apresentaremos a seguir, definições e comentários cobrados no ensino médio, ou seja: Média Aritmética,  Moda, Mediana, Variância e Desvio Padrão. Os cálculos estatísticos envolvendo as distribuições de freqüência serão vistos em cursos regulares de Estatística, na Universidade. O que será mostrado aqui será apenas uma introdução bastante elementar, tal qual os conceitos são cobrados ao nível do ensino médio.

A) Medidas de tendência central

Média Aritmética Simples - MAS: Dados  n  valores x₁, x₂, x₃, ... , x_n , chama-se média aritmética destes n valores, ao valor
M_a = (x₁ + x₂ + x₃ + ... + x_n) / n

Exemplo: qual a média aritmética de 5, 7, 6 e 8?
M = (5 + 7 + 6 + 8) / 4 = 6,5.

Média Aritmética Ponderada - MAP: Às vezes, é importante atribuir-se pesos diferenciados a cada valor, para o cálculo da média e, neste caso, a média recebe o nome de média ponderada.
Assim, dados n valores  x₁, x₂, x₃, ... , x_n  aos quais são atribuídos os pesos k₁, k₂, k₃, ... , k_n  respectivamente, a média ponderada destes n valores será dada por:

M_p = (x₁.k₁ + x₂.k₂ + x₃.k₃ + ... x_n.k_n) / (k₁ + k₂ + k₃ + ... + k_n)

Exemplo 1: Se os valores 10, 8 e 6 possuem pesos 4, 3 e 2 respectivamente, a média ponderada destes valores será igual a:

M_p = (10.4 + 8.3 + 6.2) / (4 + 3 + 2) = 76 / 9 = 8,44.

Exemplo 2: Qual a média aritmética da distribuição de pesos de 30 alunos de uma escola conforme mostrada na tabela a seguir?

Peso (kg)	Freqüência (f)
59	2
68	10
75	7
80	9
84	2
Total	30

Solução:  a média aritmética neste caso será dada pelo quociente:

M_p = (59.2 + 68.10 + 75.7 + 80.9 + 84.2) / (2 + 10 + 7 + 9 + 2)
M_p = (108 + 680 + 525 + 720 + 168) / 30
M_p =  2201/30 = 73,36

Nota: Fazendo k₁ = k₂ = k₃ = ... = k_n = 1 na fórmula acima, obteremos:
M_p = (x₁.1 + x₂.1 + x₃.1 + ... + x_n.1) / (1 + 1 + 1 + ... + 1 )
Ora, no denominador temos o peso 1 somado n vezes e, portanto, igual a n.
Assim, teremos:
M_p = (x₁ + x₂ + x₃ + ... + x_n) / n, que é a fórmula da média aritmética. Portanto, a média aritmética simples é um caso particular da média aritmética ponderada, onde os pesos dos valores x₁, x₂, ... x_n, são  unitários, ou seja, igual à unidade.

Moda - Dados  n  valores x₁, x₂, x₃, ... , x_n , chama-se moda destes n valores, ao valor que mais se repete, ou seja, que possui maior freqüência. .
Exemplo: qual a moda do seguinte conjunto de valores:
10, 10, 10, 10, 10, 20,
20, 35, 35, 35, 78, 78,
78, 78, 78, 78, 78, 78,
78, 90, 90, 90, 92, 94 ?
Resposta: M₀ = 78, porque é o mais repetido, ou seja, 78 é o valor de maior freqüência.

Observe que estes dados poderiam ser tabulados da seguinte forma:

Valor	Freqüência
10	5
20	2
35	3
78	9
90	2

onde na coluna freqüência estão indicados os números de repetições de cada valor. Nota: um conjunto de valores pode ter mais de uma moda ou até não ter nenhuma. No caso do conjunto possuir apenas uma moda ele é dito unimodal.

Mediana – Dados  n  valores x₁, x₂, x₃, ... , x_n , ordenados de forma crescente ou decrescente, chama-se mediana destes n valores, ao valor que ocupa a posição central.
Exemplo: a mediana do seguinte conjunto de valores:
12, 14, 16, 18, 20, 22, 24, 26, 28  é  igual a 20, pois 20 é o valor central.
Se o número de elementos do conjunto de valores for par, a mediana será igual à média aritmética dos dois termos centrais.
Exemplo: a mediana do conjunto de valores 12, 14, 16, 18, 20, 22, 24, 26, 28, 30 será igual a M_e = (20 + 22) / 2 = 42/2 = 21.

B) Medidas de dispersão

Desvio médio – Seja o conjunto de valores x₁, x₂, x₃, ... , x_n  e seja M_a a média aritmética desses valores. Sendo D_i o desvio médio do valor x_i, define-se:
D_i = x_i – M_a

Exemplo: Seja o conjunto de valores 10, 10, 12, 12, 12, 14, 16, 18 , 20, 20.
A média aritmética desses 10 valores será igual a:
M_a = (10+10+12+12+12+14+16+18+20+20) / 10 = 144 / 10 = 14,4
Por exemplo, o desvio médio do valor 10 , será igual a 10 – 14,4 = -4,4.
O desvio médio do valor 14 será igual a 14 – 14,4 = -0,4
O desvio médio do valor 18 será igual a 18 – 14,4 = +3,6 e assim sucessivamente.

Variância - Seja o conjunto de valores x₁, x₂, x₃, ... , x_n  e seja M_a a média aritmética desses valores. Sendo D_i o desvio médio do valor x_i, define-se a variância deste conjunto como sendo a média aritmética da soma dos quadrados dos desvios médios.

Como o conjunto x₁, x₂, x₃, ... , x_n  possui n elementos, a variância v será calculada pela fórmula a seguir, decorrente da definição acima:


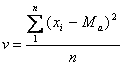
A fórmula acima pode parecer um pouquinho estranha. Caso necessário, visite o arquivo sobre somatórios.
Vamos dar um exemplo para desmistificá-la:
Seja o conjunto de  valores: 10, 12, 14, 16, 18, 20
A média aritmética destes valores será: M_a = (10+12+14+16+18+20)/ 6 = 90/6 = 15
Os desvios médios serão:
D₁ = 10 – 15 = -5
D₂ =  12 – 15 = -3
D₃ = 14 – 15 = -1
D₄ = 16 – 15 = 1
D₅ = 18 – 15 = 3
D₆ = 20 – 15 = 5
Então a variância V será igual a:

V = [(-5)² + (-3)² + (-1)² + 1² + 3² +5²] / 6 = 70 / 6 = 11,67

Desvio padrão – chama-se desvio padrão s de um conjunto de valores, à raiz quadrada da variância, ou seja, s = Öv. Assim, por exemplo, o desvio padrão do conjunto de valores dado no exemplo acima será igual à raiz quadrada de 11,67 , ou seja,  
Ö11,67 = 3,42.
A fórmula para o cálculo do desvio padrão de um conjunto de valores x₁ , x₂, x₃, ... , x_n  de média aritmética M_a será dada por:

Notas:
a) s : símbolo para representar o desvio padrão; letra grega  sigma minúscula
b) S : símbolo para representar somatório ; letra grega sigma maiúscula.
c) se ocorrer x₁ = x₂ = x₃ = ... = x_n , os desvios médios x_i – M_a serão nulos e, neste caso, o desvio padrão será nulo. Aliás, esta é a única forma do desvio padrão ser nulo.

Exemplo: calcule o desvio padrão da distribuição de freqüência a seguir:

Produto	Preço unitário (R$)
A	10,00
B	12,00
C	14,00
D	16,00

Inicialmente, calculamos a média aritmética dos dados:
M_a = (10 + 12 + 14 + 16) / 4 = 13, ou seja, a média aritmética dos preços é igual a R$13,00
Em seguida calculamos os desvios médios e os seus quadrados:
10 – 13 = -3  ? quadrado = (-3)² = 9
12 – 13 = -1 ? quadrado = (-1)² = 1
14 – 13 = +1 ? quadrado = (+1)² = 1
16 – 13 = + 3 ? quadrado = (+3)² = 9
Calculamos a variância:
v = (9 + 1 + 1 + 9) / 4 = 5
O desvio padrão será igual então à raiz quadrada da variância ou seja:
s = Ö5 = 2,23 .
Nota: a unidade do desvio padrão é a mesma da média. Portanto, s = R$2,23.

Nota: quanto maior o desvio padrão, maior o grau de dispersão dos dados de um determinado conjunto de valores ou seja, quanto mais assimétricos os dados, maior o desvio padrão. Somente a título de exemplo ilustrativo, considere os casos simples abaixo:
a) valores 4 e 6: média aritmética = (4+6)/2 = 5 e desvio padrão = 1.
b) valores 4 e 10: média aritmética = (4+12)/2 = 8 e desvio padrão = 4.
Observe que os dados 4 e 6 são mais “homogêneos” que os dados 4 e 12 (maior assimetria no segundo caso) e o desvio padrão do segundo conjunto de valores é bem maior que o do primeiro. 

Coeficiente de variação – se um dado conjunto de valores possui média aritmética M_a e desvio padrão s define-se o coeficiente de variação C_v como segue: 

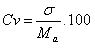
Por exemplo, no caso anterior a média aritmética dos valores é igual a 15 e o desvio padrão é igual a 3,42. O coeficiente de variação será igual a (3,42/15).100 = 22,8%.

Nota: o uso do coeficiente de variação permite a comparação dos graus de dispersão de duas ou mais distribuições de freqüência .

Exemplo: Considere que numa sala de aula se tenha calculado a média aritmética das alturas (em centímetros) e dos pesos dos alunos (em quilogramas) e os seus respectivos desvios padrões, e se tenha obtido os seguintes resultados:
Alturas: M_a = 175 cm e  s = 10 cm
Pesos: M_a = 60 kg e s = 6 kg.
Qual dos dois conjuntos de dados apresenta maior dispersão em relação à média?

Isto poderá ser respondido através do cálculo do coeficiente de variação para ambos os casos. Vejamos:
Alturas: C_v = (10/175).100 = 5,71%
Pesos: C_v = (6/60).100 = 10%

Como 10% > 5,71%, concluímos que a distribuição dos pesos apresenta maior dispersão do que a distribuição das alturas. Poderemos dizer então, que a distribuição das alturas é mais "homogênea" do ponto de vista estatístico, do que a distribuição dos pesos na amostra de alunos dada como exemplo.

Paulo Marques, 17 de dezembro de 2006 - Feira de Santana - BA. Editado em 05/02/2011.

VOLTAR