Binômio de Newton Terceiro na UEFS em 2006

UEFS 2006-1 – O coeficiente de x⁴ no polinômio P(x) = (x + 1) (2x –1)⁶ é igual a

a) 48
b) 50
c) 64
d) 76
e) 80

UEFS - Universidade Estadual de Feira de Santana

Solução:

Supondo x ¹ - 1, teremos x + 1 ¹ 0 e, portanto, poderemos dividir ambos os membros do polinômio
P(x) por (x + 1), resultando o polinômio Q(x) seguinte:
Q(x) = P(x) / (x + 1) = (2x – 1)⁶

Veja bem : temos o binômio de Newton da forma (a + b)ⁿ ou seja (2x – 1)⁶ onde a = 2x, b = - 1 e n = 6.

Aplicando a fórmula do termo geral de um binômio de Newton ao binômio de Newton Q(x) = (2x – 1)⁶ , onde a = 2x, b = - 1 e n = 6, vem:

Repare que P(x) = (x + 1) . Q(x) = x .Q(x) + 1. Q(x) = x .Q(x) + Q(x)

Observe que como x.x³ = x⁴, teremos que calcular o termo em x³ em Q(x) [relativo à primeira parcela x .Q(x) ] e o termo em x⁴ em Q(x) [relativo à segunda parcela Q(x)].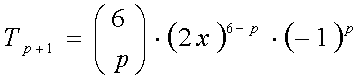
I) cálculo do termo em x³ :
Fazendo p = 3, na expressão do termo geral, fica: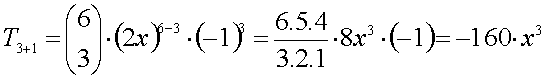

Observe que este termo T₃₊₁ = T₄ = -160x³ ao ser multiplicado por x, resultará –160x⁴ , cujo coeficiente é – 160.

II) cálculo do termo em x⁴ :
Fazendo p = 4 na fórmula do termo geral, vem: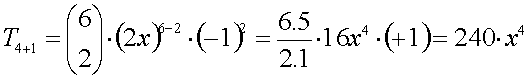



Observe que este termo T₄₊₁ = T₅ = 240x⁴ possui coeficiente 240.
Então, os coeficientes dos termos em x⁴ são iguais a –160 e 240 . A soma dos coeficientes procurada será então igual a –160 + 240 = 80. Logo, a alternativa correta é a de letra E.

Paulo Marques, 10 de fevereiro de 2006 - Feira de Santana - BA.