Nota: UESC - Universidade Estadual de Santa Cruz - ILHÉUS - BA
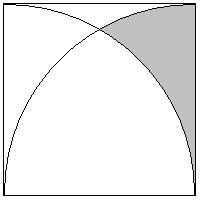
|
Geometria em São Jorge dos Ilhéus |
UESC 2007.1 – Se o lado do quadrado da figura mede x cm, então a área, em cm2 , da região sombreada é igual a
Nota: UESC - Universidade Estadual de Santa Cruz - ILHÉUS - BA
01) (x2/12)
(3Ö3 - 2p)
02) (x2/12) (3Ö3 +p)
03) (x2/12) (3Ö3 - p)
04) (x2/4) (3Ö3 + p)
05) (x2/4) (3Ö3 - p)
Solução:
Considere a mesma figura
reproduzida abaixo com a indicação das letras e
de um triângulo BPC, para facilitar a visualização
da solução.
Observe que sendo APC
um arco de circunferência, a medida do segmento BC é
igual à medida do segmento BP (BP e BC são raios do arco de
circunferência). Analogamente, pelo mesmo raciocínio,
sendo BPD um arco de circunferência, a medida do segmento BC é
igual à medida do segmento PC. Então temos: BC = BP e
BC = PC.
Ora, podemos concluir então que BC = BP = PC = x
e, portanto o triângulo BPC é eqüilátero.

Sendo o triângulo
BPC eqüilátero, seus ângulos internos valem 60º.
Como o ângulo BCD é reto em C (90º), concluímos
que o ângulo PCD vale 30º. Nestas condições,
para calcular a área da região sombreada, basta
calcular a área do setor circular de 30º ( S1
) e subtrair desta a área do segmento circular ( S2
) (parte hachuriada da figura).
I – cálculo
da área S1 do setor circular de 30º
Regra de três simples
direta
360º ........................................ p
. x2
30º ........................................ S1
Daí tiramos S1
= (p . x2 . 30) / 360 = (p
. x2) / 12
II – cálculo da área
S2 do segmento circular (parte hachuriada da figura)
a) calculamos a área
do setor circular de 60º e subtraimos desta a área do
triângulo BPC.
Área do setor circular de 60º
: analogamente ao item I, esta área será igual a
(p
. x2 . 60) / 360 = (p . x2)
/ 6
A área do triângulo eqüilátero
BPC será igual a (x2 . Ö3)
/ 4
Portanto, a área do segmento circular S2
será igual a:
S2 = [(p
. x2) / 6] – [(x2 . Ö3)
/ 4]
Então, a área procurada será

Simplificando a expressão
acima, vem finalmente:
Portanto, a alternativa
correta é a de número (03) Nota elucidativa para entender uma das passagens acima na solução do problema:
A área S de um triângulo equilátero de lado L é igual a
Paulo
Marques, 27 de janeiro de 2007
VOLTAR