1 - Entende-se por mediana de um triângulo ABC, como sendo o segmento de reta que une um dos vértices do triângulo, ao ponto médio (metade do comprimento) do lado oposto.
Como qualquer triângulo possui três vértices ( A, B ou C) , infere-se (deduz-se) daí , que um triângulo qualquer possui certamente três medianas. Estas medianas encontram-se (sempre) num único ponto, denominado baricentro ou centro de gravidade do triângulo.
Na figura abaixo, onde AM = MC, (M é o ponto médio de AC) , BM é a mediana relativa ao lado AC. Repare que os triângulos ABM e BMC possuem bases de medidas iguais (AM = MC) e também possuem a mesma altura, tendo por conseqüência, a mesma área. (lembre-se que a área de um triângulo é igual à metade do produto da base pela altura).
Daí, conclui-se que a mediana relativa a um lado de um triângulo, o divide em dois outros triângulos de áreas iguais. Saiba que esta é uma conclusão importante.

Supondo por exemplo que na figura acima, o triângulo ABM (sendo BM uma mediana do triângulo ABC) tenha área igual a 15 u.a., poderemos afirmar que o triângulo BMC também terá área igual a 15 u.a. (u. a . = unidades de área). A área do triângulo ABC será então 15 + 15 = 30 u.a.
2 – O baricentro (ou centro de gravidade) de um triângulo, é, justamente, o ponto de interseção das três medianas do triângulo. Sabe-se (e isto pode ser provado) que o baricentro (ponto G) de qualquer triângulo, situa-se a 2/3 do comprimento da mediana relativa ao lado considerado.

Assim é que na figura acima, teremos:
CG = (2/3).CE , AG = (2/3).AF , BG = (2/3).BD, onde D, E e F são os pontos médios dos lados. Também da figura abaixo: Como (2/3) + (1/3) = 3/3 = 1, é trivial concluir que
GE = (1/3).CE , GF = (1/3).AF e GD = (1/3).BD .
Exercício resolvido I: Dado o trapézio retângulo ABCD da figura abaixo, pede-se calcular a área do triângulo ABC, sabendo-se que CE é uma mediana do triângulo CDA.
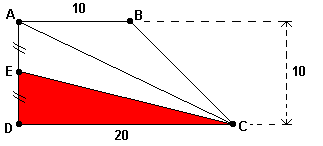
Solução: Como CE é mediana, E é ponto médio de AD. Como AD mede 10, teremos que DE = EA = 5. Também, pelo fato de CE ser uma mediana, as áreas dos triângulos CDE e CEA são iguais. Portanto, como o triângulo EDC é retângulo em D, a sua área será igual a (20.5) / 2 = 50 e, por conseqüência, a área do triângulo CEA será também igual a 50. Concluímos então que a área do triângulo CDA será igual a 50 + 50 = 100.
Para achar a área do triângulo ABC solicitada no problema, basta calcular a área do trapézio ABCD e subtrair a área do triângulo CDA que já sabemos ser igual a 100.
A área do trapézio é dada por S = [(base maior + base menor).altura] = [(20 + 10).10] / 2 = 150.
Portanto, a área do triângulo ABC será igual a 150 – 100 = 50 u. a . (u. a . = unidades de área).
Exercício resolvido II: Considerando o trapézio retângulo dado na figura abaixo, pede-se calcular o comprimento FC = x, sabendo-se que as áreas dos quadriláteros ABFE e EDCF são iguais.
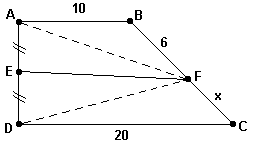
Solução:
Seja S1 a área do triângulo ABF, S2 a área do triângulo AEF, S3 a área do triângulo EFD e S4 a área do triângulo DFC. Do enunciado, poderemos escrever: S1 + S2 = S3 + S4 .
Sendo FE uma mediana, já sabemos que as áreas dos triângulos EAF e EFD são iguais, ou seja: S2 = S3. Então, a igualdade S1 + S2 = S3 + S4 simplificada fica: S1 = S4, uma vez que os termos S2 e S3 por serem iguais, se cancelam.
Vamos calcular as áreas S1 e S2, usando o teorema das áreas, segundo o qual, a área de um triângulo é igual ao semi-produto de dois lados pelo seno do ângulo que eles formam entre si. Teremos então:
S1 = S4 \ (1/2) . 10 . 6 . sen B = (1/2) . x . 20 . sen C
Como a figura dada é um trapézio, as bases são paralelas ou seja, AB // DC e, portanto, os ângulos B e C são suplementares, ou seja B + C = 180º \ B = 180 – C .
Substituindo, vem:
(1/2). 10 . 6 . sen(180 – C) = (1/2) . x . 20 . sen C
Já sabemos da Trigonometria que sen(180 – C) = sen C. Portanto, poderemos escrever:
(1/2).10.6.senC = (1/2).x.20.senC
Cancelando o termo comum senC e simplificando, resulta:
30 = 10x , de onde tiramos x = 3.
Agora resolva estes:
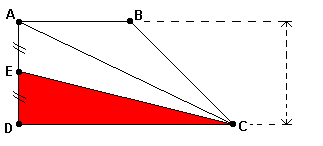
1) No trapézio retângulo da figura abaixo, pede-se calcular a área do triângulo ABC , sabendo-se que AB = 8 cm, DC = 12 cm e AD = 10 cm e que E é o ponto médio de AD.
Resposta: 40 cm2
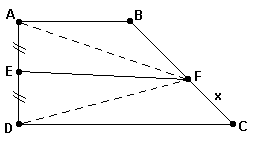
2) No trapézio retângulo da figura abaixo, pede-se calcular o comprimento FC = x, sabendo-se que as áreas dos quadriláteros ABFE e EFCD são iguais e que AB = 14 cm, DC = 20 cm e BF = 10 cm.
Resposta: x = 7 cm
Paulo Marques, 12 de junho de 2004, Feira de Santana - BA.