Veja a figura 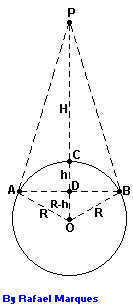 , acima onde:
, acima onde:
A Terra vista do espaço
Calcular o percentual da superfície da Terra visto por um astronauta posicionado a uma altura H em relação ao solo. Suponha que a Terra seja esférica e possua raio R.
Solução:Veja a figura
, acima onde:
H = distancia do astronauta ao solo
R = raio da Terra
Sendo P a posição do astronauta, a visão dele será uma calota esférica de altura h.
Nota: uma analogia apenas para lembrar: se você partir uma laranja em duas partes, ficarão definidas duas calotas , que serão as superfícies das cascas de cada uma das partes da laranja. Observe que calota não é um sólido e sim, uma superfície. Portanto, calota não possui volume e sim, área.O percentual da superfície da Terra visto pelo astronauta, será igual ao quociente da área da calota esférica pela área total da esfera , multiplicado por 100 (para o resultado ser em %).
Ora, a área de
uma calota de altura h numa esfera de raio R é
dada por
Sc = 2pRh
e a área de uma esfera de raio R é dada por Se
= 4pR2 .
Portanto, o percentual da superfície vista pelo astronauta será %p dada por:
%p = (Sc /
Se).100 = 100.Sc / Se
Nota: A
multiplicação por 100 na igualdade acima é para
o resultado ser expresso diretamente em porcentagem.
Substituindo Sc
e Se pelas expressões vistas acima, vem:
%p = (100.2pRh)
/ (4pR2) .
Simplificando, vem:
%p
= (50h) / R onde %p é a
percentagem procurada.
Precisamos calcular
então a altura h da calota. Vamos então, nesta
direção.
Considerando que os
segmentos PA e PB são tangentes à circunferência
(ver figura acima), podemos concluir que PB é perpendicular a
OB e, portanto, o triângulo OPB é um triângulo
retângulo. No triângulo OPB, temos os catetos OB e PB e a
hipotenusa OP.
Sabe-se que dado um triângulo retângulo
de hipotenusa a e catetos b e c e sendo m
a projeção do cateto b sobre a hipotenusa e
sendo n a projeção do cateto c sobre a
hipotenusa, podemos escrever: b2 = am e c2
= an .
Então, no triângulo retângulo OPB da figura acima, poderemos escrever:
OB2 = OP.OD
Substituindo OB = R , OP = H + R OD = R – h (olhe com atenção especial a figura acima para concluir isto), teremos:
R2 = (H +
R)(R – h)
Desenvolvendo a igualdade acima:
R2 = HR –
Hh + R2 – Rh
R2 – HR + Hh –
R2 + Rh = 0
Hh – HR + Rh = 0
Hh + Rh = HR
Colocando h em
evidencia, h(H + R) = HR
Daí, tiramos: h = HR /
(H+R)
Como já vimos acima que %p = 50h / R, vem,
substituindo:
%p = 50[(HR / (H+R)] / R = 50HR / R(R+H) = 50H /
(R + H)
Portanto, o percentual %p da superfície da
Terra visto por um astronauta posicionado a uma altura H em relação
ao solo será dado por %p
= 50H / (H + R) onde R é o raio da Terra,
considerada esférica.
Considerando-se que o valor
aproximado do raio da Terra é 6400 km, teremos:
%p @
50H / (6400 + H) onde o símbolo @
significa igual aproximadamente a .
Assim, por exemplo,
para uma altura de H = 100 km, resultaria
%p = 50.100 /
(6400+100) = 5000 / 6500 @ 0,77%
da superfície da Terra seria vista.
Para H = 1000 km ,
teríamos %p = 50.1000 /(6400+1000) @
6,76% e assim por diante.
Poderemos então construir a
tabela abaixo com base na fórmula
%p
@
50H / (H + 6400):
H (em km)
%p
1
0,0078%
10
0,0780%
100
0,7692%
1000
6,7567%
10000
30,4878%
100000
46,9925%
Observe que se H
for muito maior do que 6400 km, poderemos dizer que H + 6400 @
H e a fórmula acima se resumiria a %p = 50H / H = 50%. Isto
significa que se a altura H tender para o infinito, o percentual de
visão vai tender para 50%, ou seja, a metade da área
total da Terra poderá ser vista.
Agora
resolva este:
Calcular o percentual da superfície
da Terra visto por um astronauta posicionado a uma altura R em
relação ao solo. Suponha que a Terra seja esférica
e possua raio R.
Resposta: 25%
Paulo
Marques, 23 de fevereiro de 2003, Feira de Santana - BA.
VOLTAR